DDPM(Denoising Diffusion Probabilistic Model)是基于扩散模型的里程碑的模型,这篇文章将向大家介绍DDPM模型的数学原理以及相关实验实践方法。在介绍原理的过程中,尽可能针对公式做一些详细的介绍,在介绍的过程中,作者本人对于相关算法的过程理解也会更加的深入,和相关感兴趣的读者一样,知识和相关原理的认识是一个不断加深的过程,希望在介绍这些技术原理的同时,自己也能有更多的进步,也希望对相关的读者有所帮助。
DDPM借鉴了非平衡热力学的相关思想,系统从一个无序(完全高斯随机噪声,高熵)的结构逐渐变成一个有序(低熵)的结构(图像等)。下面将介绍这个过程的一些相关的数学方法和流程。
DDPM有前向和逆向过程,前向是从有序到无序的过程,通过不断的向数据样本中添加随机噪声使得数据一般的清晰图像到随机的高斯噪声(熵增过程)。具体公式为(其中beta的取值范围为0-1之间,但随着时间不断增大,亦即模糊化的过程越来越快,关于beta随着时间t的变化可以有不同的scheduler去生成,如线性的,二次的或余弦的):
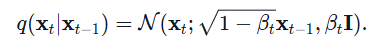
上述公式可以通过一个均值为0,方差为1的高斯采样(如果是二维图像数据,则所有像素都是独立同分布采样)生成的随机数eposilon来组合生成,其公式表示为:
上述t时刻的状态在t-1时刻已知的情况下,和t-1时刻之前的状态无关,因此我们也称为这个前向的加噪的过程为马尔可夫链过程。接下来将以问答的形式来介绍后续的相关原理。
问题1:有快速生成t时刻和t+1时刻的样本的方法吗?
回答:可以确认有快速生成t时刻样本的方法,而不需要经过t次高斯随机函数的迭代计算,这种方法称为重参化技巧(The reparameterization trick)。具体公式描述为:
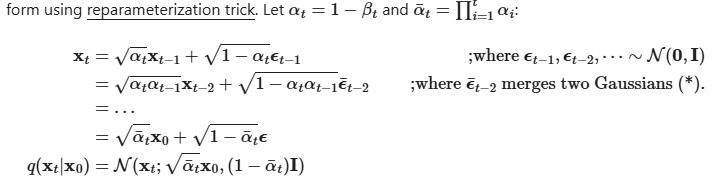
对上述公式的推导过程解释如下,第二行是基于t-1时刻的数据由t-2时刻的数据加噪声生成而来,将第一行的t-1时刻的数据通过t-2时刻的数据生成去替代而得出:
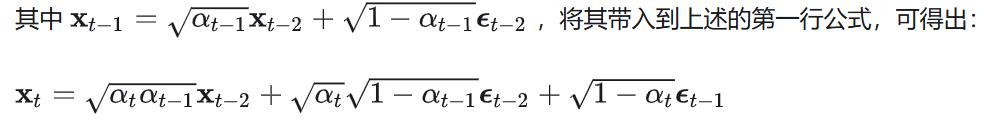
图3公式的后两项为两个均值为0的高斯分布的叠加,epsilon前的系数分别为两个高斯的标准差,根据高斯分布叠加原理,叠加后的高斯分布的方差为两个高斯分布的方差之和(根据高斯概率分布的公式推导)。因此得出图2第二行的第二项,epsilon bar表示叠加后的高斯分布。依次类推得出最后的结果。因此通过t个步骤的叠加后,噪声数据仍表现为高斯分布,当步骤T足够大时,不断加噪后生成的样本数据XT将服从均值为0(无限接近0)的标准随机高斯分布(因为图2中的x0的系数接近于0)。
问题2:前向加噪的过程是已知的概率分布(高斯概率分布函数已知),而生成的过程从各向同性的完全随机高斯分布的高熵数据情况开始,其逆过程为去噪的过程。逆过程为什么也服从高斯分布?逆过程的求解过程怎样,是否只要学习到逆过程高斯分布的噪声就可以进行递推迭代了呢?
关于逆向过程也可以近似为高斯分布的原因也可以从多个角度进行解释,比如1、从t-1到t的加噪过程可以近似的看成是线性的变换加一个小的噪声,影响较小,可以近似为高斯分布;2、根据贝叶斯公式的变换,同时t-1时候的x(先验分布)也可以近似的看成是高斯分布(根据高斯概率公式的推导,两个高斯分布的乘积仍是高斯分布)。由于在训练时,我们是已知0时刻的原始样本x的,因此在原始样本x0已知的情况下,从t时刻到t-1时候的变化概率可以用如下公式进行建模。
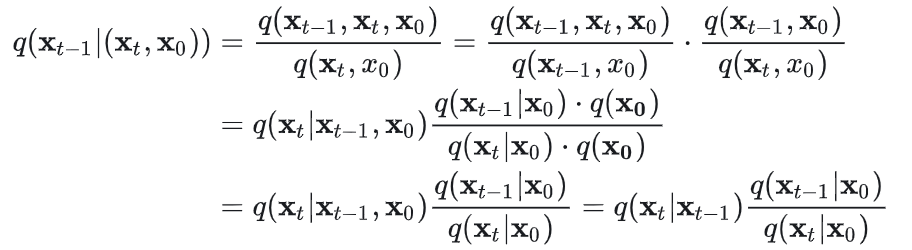
上述公式是三个前向高斯分布的运算,具体的运算过程可以参考引文1,其利用到了高斯分布是自然指数函数,利用了指数函数运算特性进行的公式推理。
既然逆向过程的每一步变化也服从小的扰动的高斯分布,关键是怎么学习到这样的分布,即均值和方差,在这里主要就是构建一个神经网络,通过输入t时刻的x和t时间特征,就能输出对应的均值和方差。在学到误差之后,就可以通过t时刻的x和误差以及相关的超参数去构造t-1时刻的x,其公式表达如下,其中epislon为学习到误差,sigma(theta)为方差表达式,具体公式的推导可以参考引文1中的详细描述。因此逆向过程可以理解为系统学习到了从无序到有序构建过程的数学模型结构和构建流程算法。
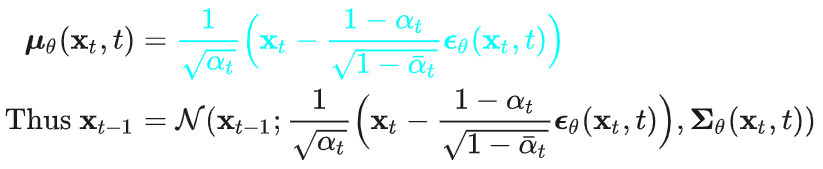
问题3:用图4以及图5的公式去构建逆向扩散过程的数学原理根据是什么?
回答:上述逆向构建扩散过程的原理在于可以基于公式推导出通过优化VLB,找出其接近的下界,间接的优化了数据x(0)的最大似然,或其CE(cross entroy),因为最大似然和CE的相关loss都是小于VLB的。VLB求得最小,可以理解为其间接优化了我们的目标损失函数。具体的VLB的求解过程可以通过参考引文1中的公式推导,最终的结果(从x(t)到x(t-1)的转换)等同于求解图4的条件概率。
References
Leave a Reply