图(graph)相关的数据结构在解决实际问题时也会常用到,这里向读者介绍几个相关应用题目并给出解决思路分析和代码实现,欢迎读者朋友们针对相关问题提出意见和建议,用更好的思路和更加高效的方法去解决。
问题1:参考引文1的描述(这里就不再花文字描述问题本身),理解题目确实要花点时间,这里用图示辅以简单的文字重复描述一下,如下图所示,方格编号从左下角开始连续交错方向按数字递增进行编码,下图的示例对应着如下的输入数据:输入:board = [[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,35,-1,-1,13,-1],[-1,-1,-1,-1,-1,-1],[-1,15,-1,-1,-1,-1]]。可以看出从最后一行开始,第二个格子的数字为15,意思是从2到15(第四行第三列)安排了一个梯子或蛇,可以直接传送不算挪动的步骤,这样到达目标所在地分别是从1->2,15->17,13->14,35->36,四步即可到达。
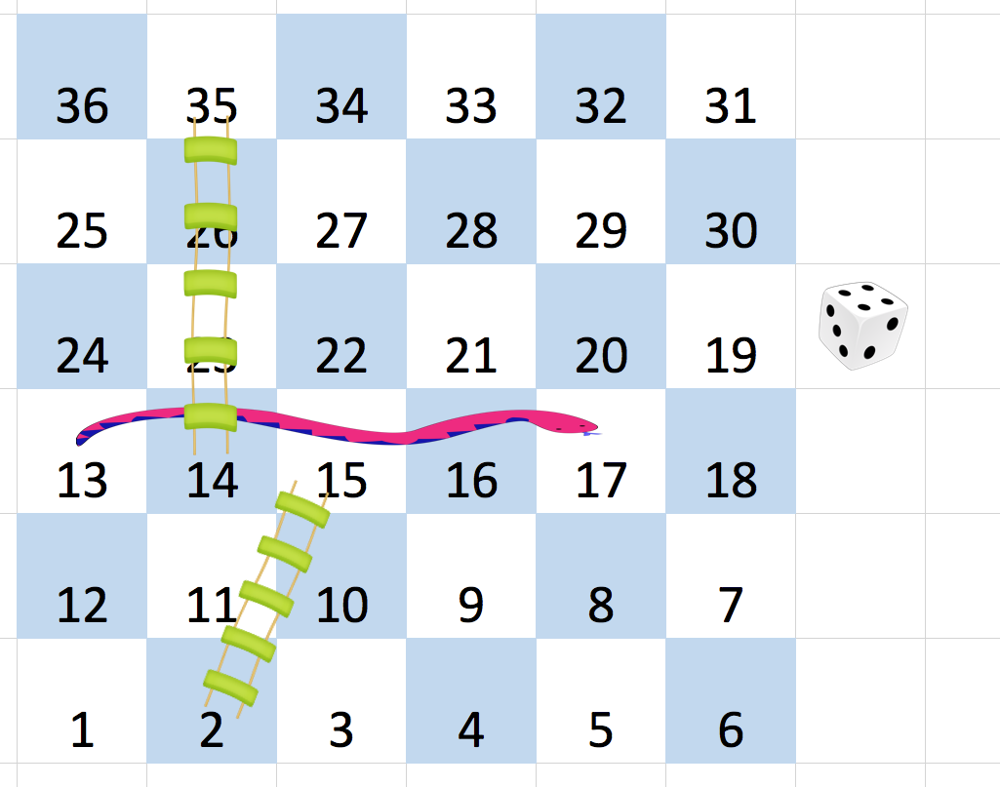
首先,我们来分析一下题目的含义和根据场景用合适的数据结构建模相关问题,首先根据board去解析数据,构造合理的数据结构和算法解决问题。我们可以看到目标方格 next的编号符合范围是[curr + 1, min(curr + 6, n2)],可以理解为从curr(当前方格的位置索引)到这些范围内的任何一个值都存在着一条边(等值边,边长为1,没有长短优先级),比如1到2-7这些格子都可以直接到达,因此我们可以将这个问题构建为一颗动态的搜索图。从根节点位置1开始,如存在着节点有梯子和蛇,则同时添加一条curr到梯子或蛇的终点位置编号的边(不需要满足next节点的1-6step的约束,而且这里特别注意一下,规则中说明梯子或蛇不能连续跳,如不能梯子跳过一些格子再连续梯子跳过一些格子),按照上述逻辑该问题为一颗有向图(如13到17存在着边,17到13也存在着边,13到17存在边时board[13]=17,17到13存在边时,即可以从位置17直接跳到13位置时board[17]=13)。
因此上述的问题就转化为了用基于图的深度优先遍历或宽度优先遍历去查找最短路径问题,搜索最短路径用宽度搜索更加合适,因为宽度搜索的过程中第一个达到目标位置的即为路径长度,而深度优先遍历算法需要遍历整个图(也存在着一些剪枝优化的行为)才能找到最短路径问题。
参考引文2提供了两个代码实现,其中第一个提供了深度优先遍历算法的实现,而且可以将搜索可能的路径都列出来,其实现主要采用了回溯递归的方法,特别需要注意的是递归过程中由于子递归返回后状态恢复的问题,由于基于深度优先遍历性能不够够,在某些测试题目上达不到时间要求,因此这道题的更为合理的方法是宽度优先遍历,采用队列结构来实现,将同一宽度的节点先后依次入队列,然后依次pop并将下一个层级的依次入栈,保证每一个访问的节点都是访问的深度最浅的某一个节点。(Solution类为基于深度优先遍历的实现,Solution2为参考的宽度优先遍历的代码,其中深度优先遍历方法做了一定的扩充,可以支持将所有可能的路径都输出出来保存到文件中)。欢迎读者对代码实现提出问题意见和建议,以便更好的去进步。
References
Leave a Reply