马尔可夫决策过程是强化学习的基本的算法,一些强化学习的概念知识点都在马尔可夫决策过程中有体现。强化学习是决策智能实现的一大类算法的统称,在游戏,智能辅助决策等场景下也有很多成功的应用。
马尔可夫性是概率论里边的一种特性,描述系统当前的状态概率只与上一个状态有关,而与之前的状态无关(或者说由于上一个状态的存在,之前的状态不会直接影响到当前状态)。用公式表示为:
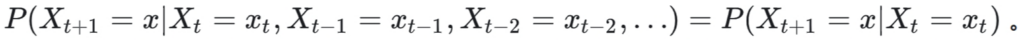
马尔可夫决策过程是对具有离散状态的环境下的决策行为序列进行优化的建模方法。在马尔可夫决策过程中,问题被建模为一个包含以下要素的数学结构:

我们通常称的策略(policy)指的是当前系统环境处于s的情况下,采取某种行为a去执行,这种根据状态去执行特定的行为称为策略,一个策略下的价值函数(value function)定义为:
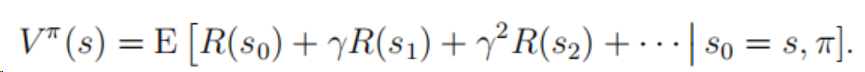
其中s为起始状态,pi为策略,因为在状态s下执行策略pi后下一个状态是概率分布,因此上述公式是期望值。价值函数更有价值的公式为下面的贝尔曼方程。其为一种递归定义:
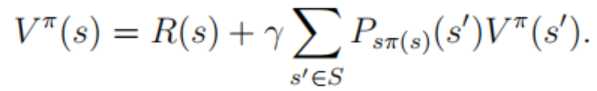
上述公式的最右边可以理解为在当前状态为s的情况下执行策略pi后到达状态s’(满足上述的转移概率)后的价值函数,因为是满足概率分布,所以在不同s‘下求得价值函数的期望值即为结果。最优价值函数即为获取价值最大的策略。这里只关心其贝尔曼方程的表达(因为其方便用程序来实现,后面链接会有相关示例代码去进一步加深理解)。
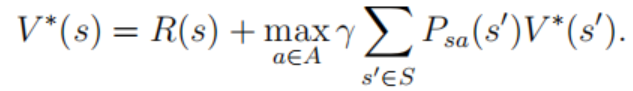
通过上述的价值函数和最优价值函数的递归定义,我们就可以通过迭代算法去找到最优价值函数,并同时能找到其对应的最优策略。这里介绍两种迭代算法来找出最优的策略,第一种为policy iteration,第二种为value iteration。policy iteration首先通过迭代算法找出最优价值函数,然后通过迭代找出最优策略,而value iteration则是直接在迭代找出最优价值函数的过程中同时将最优策略的逻辑一并耦合在一起。
在这里有一个简单的演示示例,为一行五个格子对应五个状态,可以想象成一个五个格子的魔方,只有一个方块,其余为空格,方块可以向左或向右移动,目标是移动到中间的格子上。我们怎么去通过上述的迭代方法找出最优策略(在每一个状态下执行向左或向右行为为最优?)在这里需要注意几个关键的变量的定义,状态,当前状态价值以及状态转移矩阵。可以参考代码链接及里边的代码注解。 ai/samples/RL/MDP at master · kindlytree/ai (github.com)。
上述MDP的最优策略是在状态当前价值和状态转移矩阵已知的情况下的最优策略求解,实际过程中这些并不是已知的。这里也简要介绍一下MDP在状态转移矩阵未知情况下的求解方法,其也是基于迭代贪婪的思想,从一个随机的策略开始,然后逐步迭代找到更好的策略,在每一个中间策略迭代的开始,要做一些self play,积累一些数据,然后通过value iteration去找到更好的策略,流程伪代码如下所示:

Leave a Reply