这篇文章简要介绍一下线性代数的相关概念知识,如行列式,特征值,特征向量以及特征值分解,SVD分解等。在这里顺便记录一下以便后续查阅。
1、行列式(determinant),矩阵对应一个特定的值,一般记为det(A),余子式(minor)m_{i,j}一般记为当前矩阵去除i行j列后形成的行列式(由此也可以理解为行列式为递归定义),代数余子式(cofactor)需要在m_{i,j}的基础上再乘上一个因子(-1)^{i+j}形成c_{i,j}。同时有伴随矩阵(adjoint matrix)的概念也是基于代数余子式进行定义的。需要注意,行列式只针对于方阵。
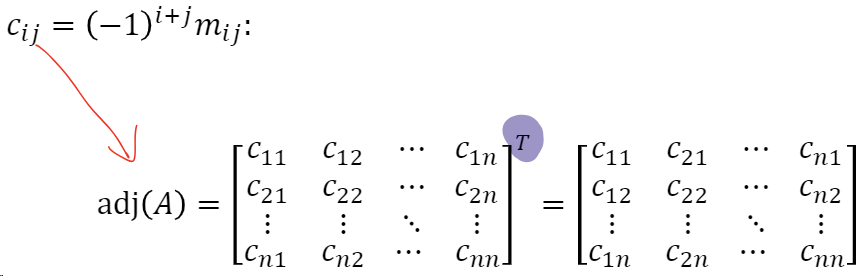
基于伴随矩阵就比较容易计算矩阵的逆。如下所示,也可以看出矩阵的逆要求其行列式不为0。
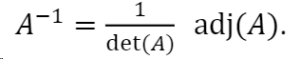
2、特征值特征向量(也是方阵,对于非方阵来说,是不存在特征值的,但是会存在条件数):满足特征方程(characteristic equatation)det(A-lamda I)=0的lambda的值即为矩阵的特征值。实对称矩阵的特征向量相互正交。特征值有其对应的代数重数(Algebraic multiplicity),每个特征值有其对应的几何重数(Geometric multiplicity,即为其对应的线性无关的特征向量的个数)。缺陷特征值(defective eigenvalue)指的是存在这个特征值的几何重数比代数重数要小的特征值。关于代数重数大于等于几何重数的相关证明,可以参考引文的链接。
3、特征值分解和SVD分解,可以参考引文3和引文4,其中特征值分解满足方阵,实对称矩阵的特征向量线性无关且为相互正交,PCA就用到了这个特性,SVD分解可以解决不是方阵的情况,但是可以通过转化为特征值分解的方法去进行求解,具体的方法可以参考引文3。特征值的计算方法可以用QR分解来进行。
References
Leave a Reply