QR分解是一种特殊的矩阵分解,将矩阵A(m,n)分解为标准正交矩阵Q(m,n)和上三角矩阵R(n,n)的乘积,QR分解可以用来求矩阵的特征值等应用。
首先解释一下施密特正交化的方法,施密特正交化将n个线性无关的向量转化为标准正交向量,其转化的步骤是首选选一个向量,然后在计算第二个向量时,将原始的第二个向量可以分解为第一个向量和垂直于第一个向量的两个向量的和。而可以利用在同一个方向上的两个向量的内积之比值即为两个向量长度的比值等特性求出第二个向量(和第一个向量垂直),以此同样的类似方法求得第三个向量,第四个向量等等。从而得出施密特正交法的公式。具体公式可以参考引文。
经过施密特正交化的方法可以得出n个标准正交的列向量,而且原始的每一个列向量都可以表示为这n个标准正交列向量的线性组合,根据施密特正交向量的生成特点,原始的列向量的线性组合的线性因子刚好符合上三角矩阵的形式。
第二种算法为Householder transformation,其依次利用列向量和标准正交基形成镜像对称的特征去找到变换的Q的关系,得出Q的特性(对称正交),具体算法请参考引文链接。
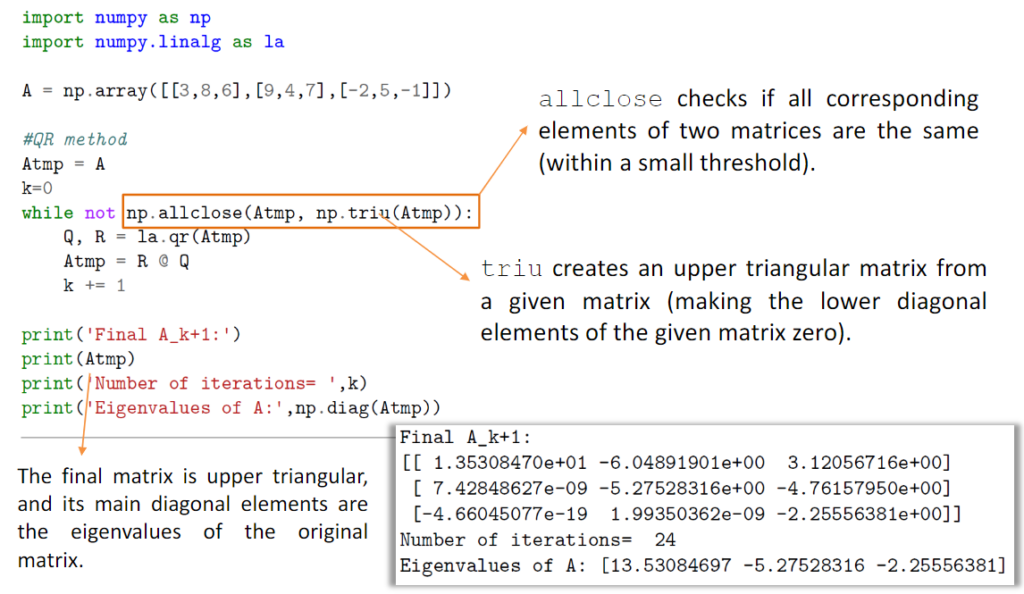
QR分解的一个用处就是用来计算矩阵的特征值,具体的原理不做特别说明,如有兴趣可以参考引文链接。下图说明了怎么用numpy基于QR分解去计算矩阵的特征值。
References
Leave a Reply