短时傅里叶分析是时频分析中经常用到的技术,由于傅里叶分析存在着时间跨度较宽导致分析结果中的频率特性中缺少了时间信息,甚至不同的信号可能会得出相同的傅里叶分析结果(如左右对称的两个信号,其傅里叶分析结果相同)。下面示例代码是短时傅里叶变换的numpy的逻辑实现,是基于局部(localized time zone)的傅里叶分析得出结果所拼接而成。其中hop_length即为短时傅里叶分析的时间分辨率。
import numpy as np
def stft(signal, window_size, hop_length):
n_frames = 1 + (len(signal) - window_size) // hop_length
stft_matrix = np.empty((window_size // 2 + 1, n_frames), dtype=complex)
for i in range(n_frames):
frame = signal[i * hop_length: i * hop_length + window_size]
windowed_frame = frame * np.hamming(window_size)
stft_matrix[:, i] = np.fft.rfft(windowed_frame)
return stft_matrix
window_size = 1024
hop_length = 512
stft_matrix = stft(signal, window_size, hop_length)
下面以一个示例来说明短时傅里叶分析不同时间窗口宽度的分析结果的效果,如下图所示为由四个不同频率的信号在连续几个时间片所组成(每个时间段由单一频率信号所组成)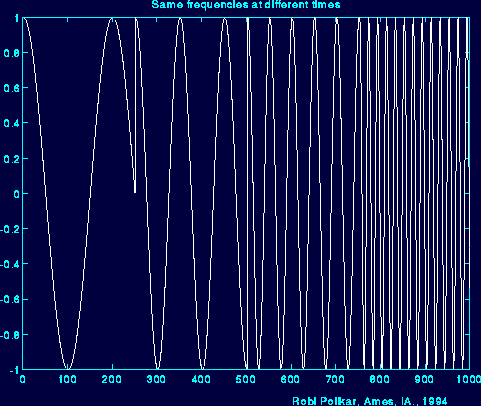
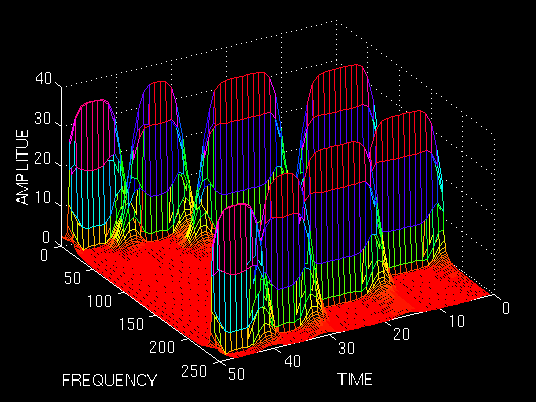
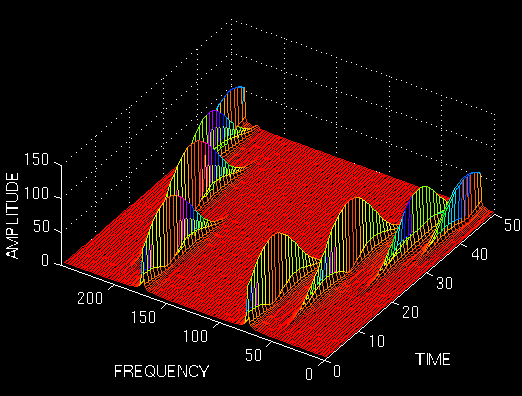
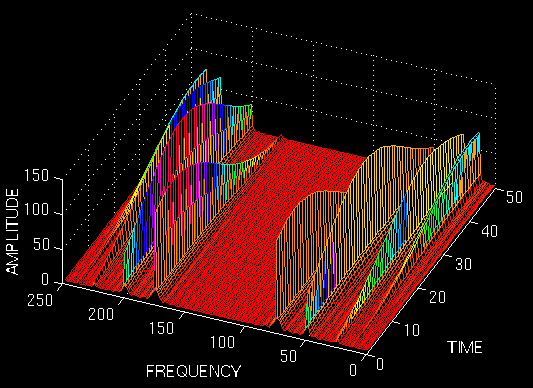
以上图示为短时傅里叶分析的三维可视化结果,也有基于二维的可视化方法,一般称为光谱(声谱)图,如下所示为一段音频的频谱分析结果(Speech spectrogram,频率大小这个维度用颜色来表示)。
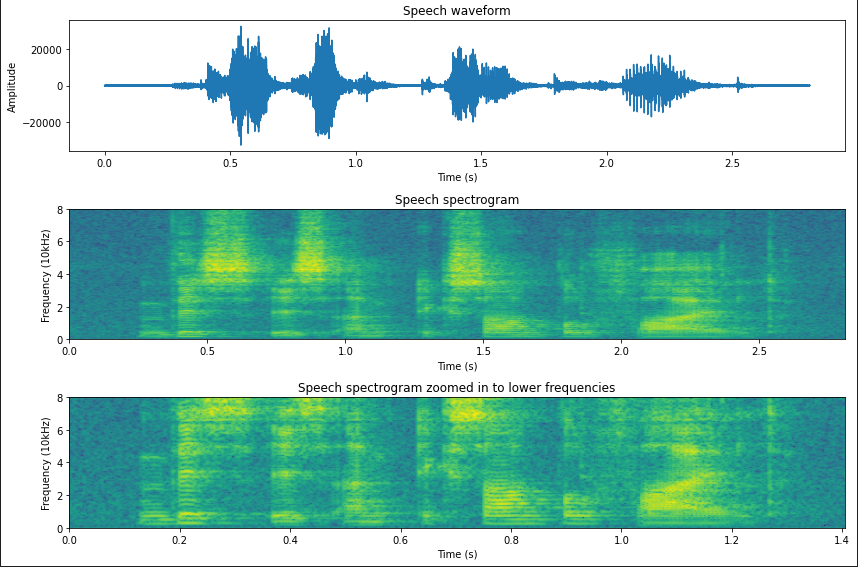
上面的声谱图可以有如下的解释:
1、基于梳状图的水平线们为对应的基频;
2、垂直线对应突然的语音信号, 通常是瞬变特征,典型的瞬变语音为辅音;爆破音;塞音;
3、在高频信号部分有较大能量的区域(更亮的颜色),一般对应着摩擦音(fricatives)
后续将继续更新光谱图的更多的分析技巧,如频率包络图等。
References
Leave a Reply